The Ultimate State Capitol Road Trip
A brute-force solution to the traveling salesman problem
Recently I read a blog post from Dr. Randal S. Olsen in which he plotted an optimal road trip to each of the lower 48 state capitols, solving what is commonly known as the “traveling salesman” problem. We consider this problem impossible to solve definitively, but it’s certainly possible to create algorithms that give a pretty good approximation. Olsen’s circular route is 13,310 miles in length. Could I do better? I thought it would be fun to try.
I’m not that great at math. So for me, an elegant algorithm full of tricky calculations wasn’t going to be the way. I needed something I could understand.
Enter Brute Force
“Brute force” is a term we use to describe programming that’s inefficient or inelegant. If it works at all, it’s only because computers are fast enough that it doesn’t matter. Brute force programming is easy to write because it works the way an average person thinks — bubble sort is the classic example. So what’s the brute force solution to this problem? Just calculate every possible route and sort them to find the shortest. Easy!
Easy, until it sinks in that the number of possible routes is 48!, approximately 1.24×10^61. To call this number large is an understatement. By comparison, there are only around 10^56 atoms in the solar system. If my computer could process a trillion routes per second, it would not even make a dent in the problem before the sun exploded. So that ain’t going to work.
What about computing routes completely at random, keeping track of the shortest one found so far? I didn’t think it would work but I was curious how close it could get. So I got a list of GPS coordinates to the capital cities and calculated the distances between each (actual math!). I decided to use the straight-line distance between the cities as an approximation and plot the result on Google Maps later to get the true driving distance.
I coded it up and ran it. Of course it spit out some huge numbers at first, 30,000+ miles. As it ran, it started finding shorter routes. I let it run overnight. By the next morning I was looking at routes near the 20k mark for distance (and I knew that the actual road route would be longer once I plotted it). I did some code optimizations but soon realized this was not going to give me the answer I wanted.
Brute Force, but Refined
I decided to revisit the idea of brute force, which I described earlier as going about the problem the way a person would. So how would a person do this? They are probably going to pick a starting point and then just go to the next closest place. Since there are only 48 starting points, it was easy to try this, and easy to see that it wasn’t the solution. When I examined Dr. Olsen’s map I could see that there are many cases where the route doesn’t in fact take you to the next closest city. A good example of this occurs in the area around Albany, which acts as a bottleneck between New England and the rest of the country.
Still, it was obvious that each city was at least connected to a nearby city. There’s no chance that an optimal route is going to have you drive from Boston to Little Rock in one shot. I changed my random route generator to pick one of the five closest points as the next destination. I added some additional optimizations such as bailing out early once the route exceeded the best found so far. I let it fly.
This worked much better. I got routes under 20,000 miles pretty fast. After a couple of hours it came up with what I call route #10639, because it has a straight-line length of 10,639 miles. When I plotted this on Google Maps and added up the driving distances, I got 13,055 miles, 255 miles better than the goal. Success!
Over the next week I made various changes to my code and ran it for a lot more hours. None of those runs produced a shorter route, and in fact most of them ended up reproducing route #10639.
The Optimal Route
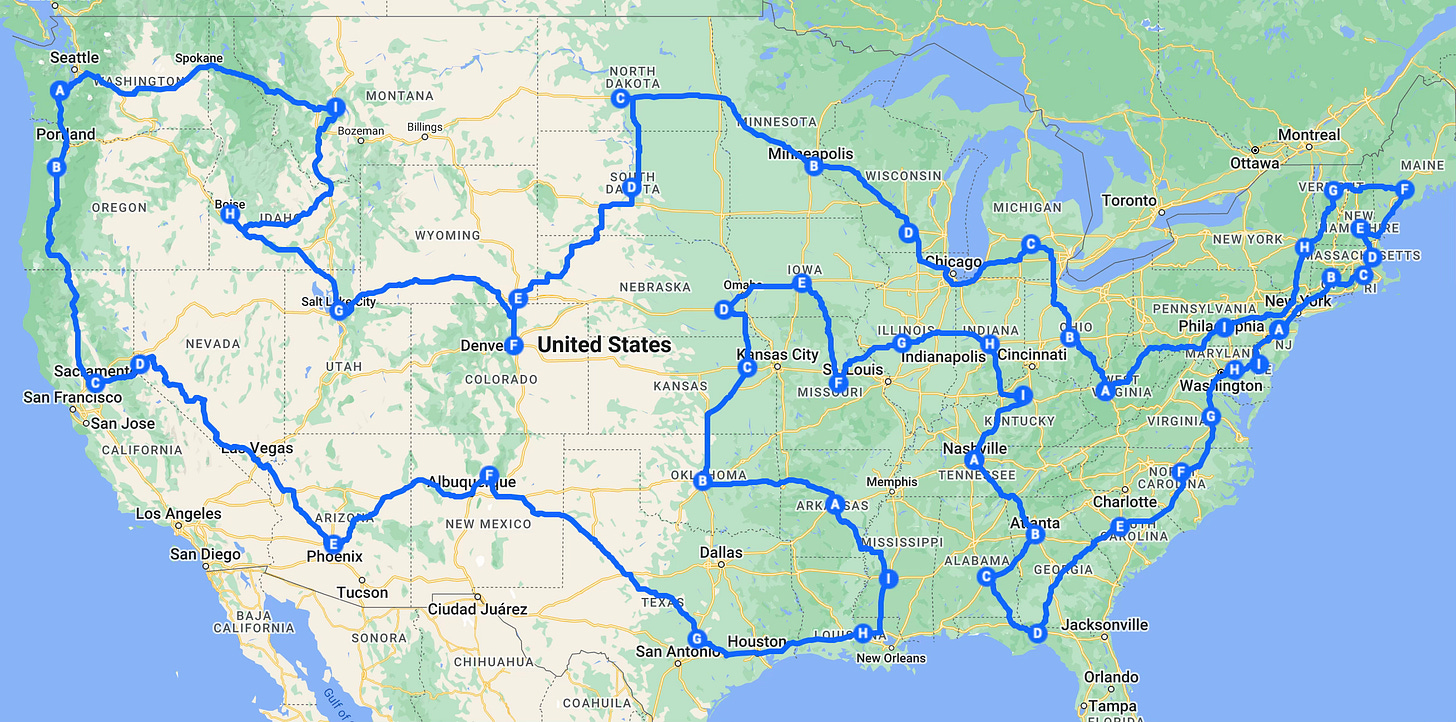
Here’s a map view of the winning route:
View the result on Google Maps to get a closer look.
For much of the route we’re traveling along the coasts or the national borders, as you might expect. The hard part is knowing when and in what order to visit the interior cities. In this solution, we cover 11 of them in a detour between Montgomery and Jackson, and the rest between Helena and Bismarck. It’s a far from obvious route, yet it emerged as the shortest among several billion alternatives.
To get this result we had to make the non-intuitive choice, on several occasions, to bypass nearby cities for more distant destinations. Indianapolis and Frankfort are only around 200 miles from their counterparts in Ohio and West Virginia, yet we don’t visit them until thousands of miles later. Harrisburg eschews its three closest neighbors, routing you to Charleston or Albany depending on your direction of travel. The detours to the interior cities could have started anywhere along the northern or southern borders.
There were two runners-up that are worth a look. Route #10652 is 13,132 miles, and route #10676 is 13,166, both shorter than the goal1. It’s interesting to compare the maps and see where they differ. Route 10652 sends you from Santa Fe to Oklahoma City instead of Austin. In 10676 we see one change in New England when visiting the three northernmost cities.
Some Technical Details
I used an M1 Mac and wrote my program in Java. Since the M1 has 8 cores, I ran 8 threads. It’s easy to do this because the threads only have to interact with each other to decide who’s currently got the best solution. I can check around 250,000 routes per second with this arrangement. ChatGPT kindly provided a list of the GPS coordinates I needed, and a function to compute the distances between them.
Each route begins at a random location and branches out from there, choosing from a list of the next N nearest destinations (omitting those we’ve already visited). I tried various values of N between 2 and 16. N=8 produces the winning route most often. If the number is too small, we miss the cases where the route bypasses a lot of nearby cities; too large, and we waste too much time looking at bad solutions. I think it might make sense to have N be dynamic and get smaller as the route is nearing its end, but I haven’t tried it.
Is there a shorter route? My intuition says that if there is, I’d have found it. Perhaps you will implement my algorithm, or something like it, and prove me wrong.
Final Thoughts
We all have computers that sit idle when we aren’t working. Long running algorithms like the one I describe here are a good way to put those resources to use for little or no extra cost2.
Most of the software problems we solve in our day to day work require fast response times, and I don’t want to discourage you from looking up and using established algorithms to solve them. But I also want you to keep in mind that there’s still room in software development for novel solutions. Don’t fall into the rut of always settling for the standard way of doing things. Someone is going to invent the next great computer algorithm that’ll change the world, and it might as well be you.
When I mapped these, I used the city names rather than the addresses of the capitol buildings, so the measurements aren’t exactly equivalent, but the difference is trivial.
An 8-core Apple M1 or M2 consumes around 30 watts at full load, which costs 50 cents per hour where I live.